#4/27(수)To_do
1.R 교과진행
-데이터분석 도구
-프레임
-분석기초
-데이터가공
2.실습 및 연습문제
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)
# 분산
var(score)
#표준편차
sd(score)
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(화) Hw_1st
#Q1 시험 점수 변수 만들고 출력하기
#다섯 명의 학생이 시험을 봤습니다.
#학생 다섯 명의 시험 점수를 담고 있는 변수를
#만들어 출력해 보세요.
#각학생의 시험 점수는 다음과 같습니다.
score=c(80,60,70,50,90,88,63,77,82,93)
score
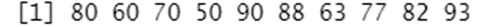
#Q2 전체 평균 분산과 표준편차 구하기
#앞 문제에서 만든 변수를 이용해서 이 학생들의 전체
#평균 점수와 분산및 표준편차를 구해보세요.
# 평균점수
mean(score)

# 분산
var(score)

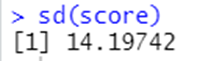
#표준편차
sd(score)
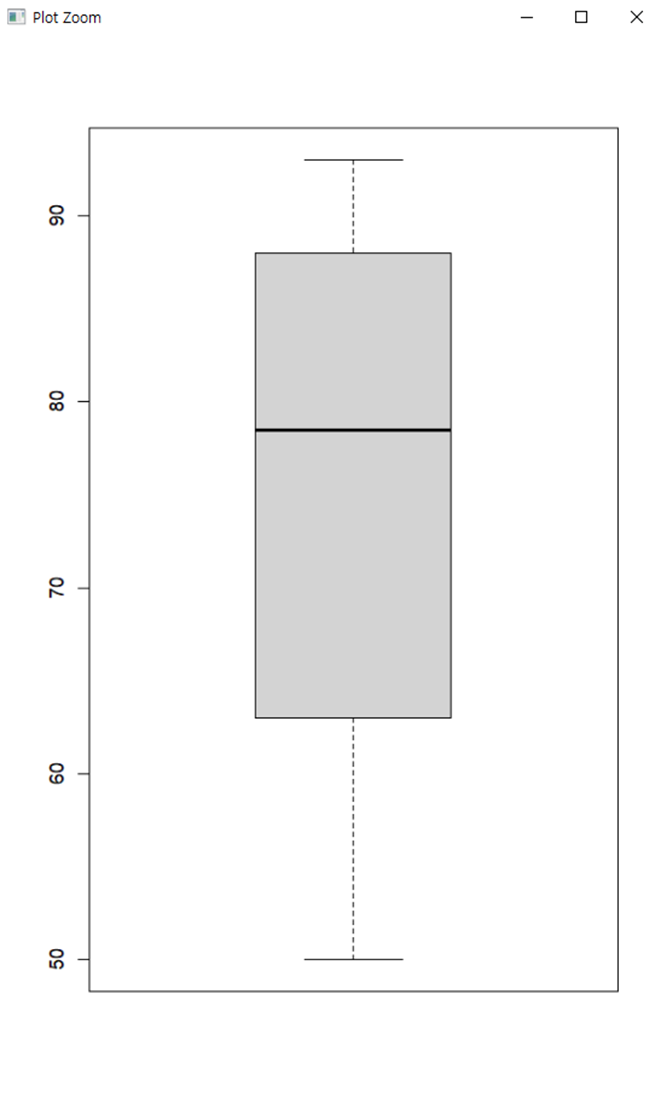
#Q3 위의 내용의 데이터를 boxplot으로 시각화 하여 작성하고
#quarter별 해당 숫자를 제시하시오?
boxplot(score)
qplot(score)
#4/27(수) HW(3rd)
#ggplot2 패키지에는 미국 동북중부 437개 지역의 인구통계 정보를 담은
#midwest라는 데이터가 포함되어 있습니다. 이를 확인하는 명령어를
#제시하고 midwest 데이터를 사용해 데이터 분석 문제를 해결해보세요.
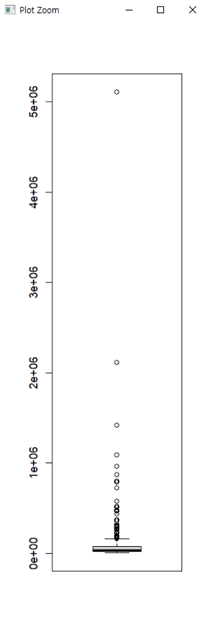
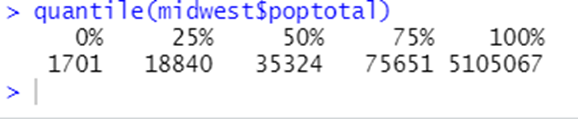
#• 문제 1. ggplot2 의 midwest 데이터를 데이터 프레임 형태로 불러와서
#boxplot()으로 데이터의 특성을 파악하세요.
par(mfrow=c(1,1))
midwest = data.frame(ggplot2::midwest)
View(midwest)
boxplot(midwest$poptotal)
quantile(midwest$poptotal)
#qplot(data=midwest$poptotal,x=midwest$country,y=midwest$area,geom="boxplot")
#• 문제 2. poptotal(전체 인구)을 total 로, popasian(아시아 인구)을
#asian 으로 변수명을 수정하시오
library(dplyr)
View(midwest)
midwest <- rename(midwest, total = poptotal)
midwest <- rename(midwest, asian = popasian)
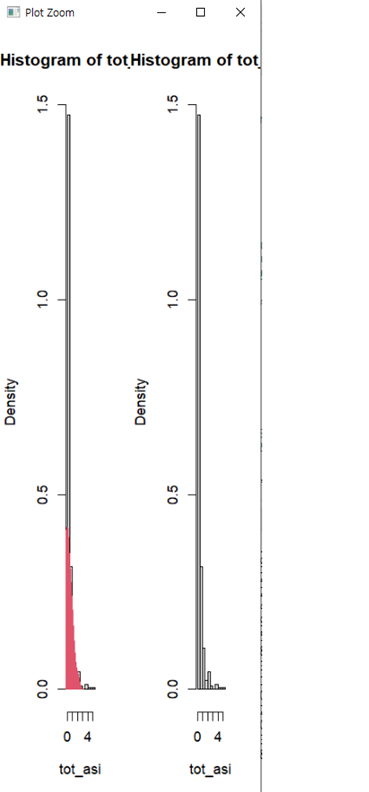
#• 문제 3. total, asian 변수를 이용해 '전체 인구 대비 아시아 인구 백분율
# 파생변수를 만들고, 히스토그램과 확률밀도를 하나의 화면을
# 2개로 분활하여 만들어 도시들이 어떻게 분포하는지 살펴보세요.
midwest$tot_asi = 100*midwest$asian/midwest$total
tot_asi
par(mfrow=c(1,2))
hist(tot_asi,probability = T)
frame()
lines(density(x),col=2,type='h',lwd=2)
#• 문제 4. 아시아 인구 백분율 전체 평균을 구하고, 평균을 초과하면 "large",
# 그 외에는 "small"을 부여하는 파생변수를 만들어 보세요.
mean(midwest$tot_asi)
midwest$group <- ifelse(midwest$tot_asi > 0.4872462, "large", "small")
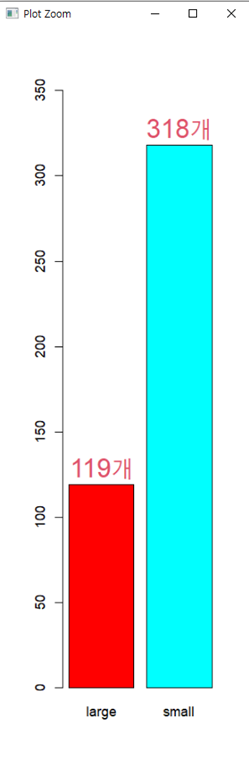
#• 문제 5. "large"와 "small"에 해당하는 지역이 얼마나 되는지,
# 막대 그래프(barplot)를 만들어 확인해 보세요.
tt=table(midwest$group)
bb=barplot(tt,ylim=c(0,350),col=rainbow(2))
par(mfrow=c(1,1))
frame()
text(bb,tt,paste0(tt,"개"),pos=3,cex=2,col=2)
#4/27(수) HW(3rd)
#ggplot2 패키지에는 미국 동북중부 437개 지역의 인구통계 정보를 담은
#midwest라는 데이터가 포함되어 있습니다. 이를 확인하는 명령어를
#제시하고 midwest 데이터를 사용해 데이터 분석 문제를 해결해보세요.
#• 문제 1. ggplot2 의 midwest 데이터를 데이터 프레임 형태로 불러와서
#boxplot()으로 데이터의 특성을 파악하세요.
par(mfrow=c(1,1))
midwest = data.frame(ggplot2::midwest)
View(midwest)
boxplot(midwest$poptotal)
quantile(midwest$poptotal)
#qplot(data=midwest$poptotal,x=midwest$country,y=midwest$area,geom="boxplot")
#• 문제 2. poptotal(전체 인구)을 total 로, popasian(아시아 인구)을
#asian 으로 변수명을 수정하시오
library(dplyr)
View(midwest)
midwest <- rename(midwest, total = poptotal)
midwest <- rename(midwest, asian = popasian)
#• 문제 3. total, asian 변수를 이용해 '전체 인구 대비 아시아 인구 백분율
# 파생변수를 만들고, 히스토그램과 확률밀도를 하나의 화면을
# 2개로 분활하여 만들어 도시들이 어떻게 분포하는지 살펴보세요.
midwest$tot_asi = 100*midwest$asian/midwest$total
tot_asi
par(mfrow=c(1,2))
hist(tot_asi,probability = T)
frame()
lines(density(x),col=2,type='h',lwd=2)
#• 문제 4. 아시아 인구 백분율 전체 평균을 구하고, 평균을 초과하면 "large",
# 그 외에는 "small"을 부여하는 파생변수를 만들어 보세요.
mean(midwest$tot_asi)
midwest$group <- ifelse(midwest$tot_asi > 0.4872462, "large", "small")
#• 문제 5. "large"와 "small"에 해당하는 지역이 얼마나 되는지,
# 막대 그래프(barplot)를 만들어 확인해 보세요.
tt=table(midwest$group)
bb=barplot(tt,ylim=c(0,350),col=rainbow(2))
par(mfrow=c(1,1))
frame()
text(bb,tt,paste0(tt,"개"),pos=3,cex=2,col=2)
#4/27(수) HW(3rd)
#ggplot2 패키지에는 미국 동북중부 437개 지역의 인구통계 정보를 담은
#midwest라는 데이터가 포함되어 있습니다. 이를 확인하는 명령어를
#제시하고 midwest 데이터를 사용해 데이터 분석 문제를 해결해보세요.
#• 문제 1. ggplot2 의 midwest 데이터를 데이터 프레임 형태로 불러와서
#boxplot()으로 데이터의 특성을 파악하세요.
par(mfrow=c(1,1))
midwest = data.frame(ggplot2::midwest)
View(midwest)
boxplot(midwest$poptotal)
quantile(midwest$poptotal)
#qplot(data=midwest$poptotal,x=midwest$country,y=midwest$area,geom="boxplot")
#• 문제 2. poptotal(전체 인구)을 total 로, popasian(아시아 인구)을
#asian 으로 변수명을 수정하시오
library(dplyr)
View(midwest)
midwest <- rename(midwest, total = poptotal)
midwest <- rename(midwest, asian = popasian)
#• 문제 3. total, asian 변수를 이용해 '전체 인구 대비 아시아 인구 백분율
# 파생변수를 만들고, 히스토그램과 확률밀도를 하나의 화면을
# 2개로 분활하여 만들어 도시들이 어떻게 분포하는지 살펴보세요.
midwest$tot_asi = 100*midwest$asian/midwest$total
tot_asi
par(mfrow=c(1,2))
hist(tot_asi,probability = T)
frame()
lines(density(x),col=2,type='h',lwd=2)
#• 문제 4. 아시아 인구 백분율 전체 평균을 구하고, 평균을 초과하면 "large",
# 그 외에는 "small"을 부여하는 파생변수를 만들어 보세요.
mean(midwest$tot_asi)
midwest$group <- ifelse(midwest$tot_asi > 0.4872462, "large", "small")
#• 문제 5. "large"와 "small"에 해당하는 지역이 얼마나 되는지,
# 막대 그래프(barplot)를 만들어 확인해 보세요.
tt=table(midwest$group)
bb=barplot(tt,ylim=c(0,350),col=rainbow(2))
par(mfrow=c(1,1))
frame()
text(bb,tt,paste0(tt,"개"),pos=3,cex=2,col=2)
'국비교육과정 > R' 카테고리의 다른 글
| [R]KoNLP 설치 (2) | 2022.04.28 |
|---|
댓글